Lyd

Grundbeskrivelse 

Lyd i luft udbreder sig som en longitudinalbølge (Christophe Dang Ngoc Chan, Wikimedia Commons)

Vi forstår normalt lyd som en bølgebevægelse, der breder sig i en gas. Det kan imidlertid også være bølgebevægelse i væsker og faste stoffer. I gasser og væsker breder lyden sig som en såkaldt longitudinalbølge, dvs. en bølge, hvor udbredelsesretningen er den samme som svingningsretningen. Bølgen indeholder energi, som følger bølgen.

I luft breder lydbølgen sig med en fart på v = 343 m/s ved 20˚C. Ved højere temperaturer breder lyden sig hurtigere, i gasser med store molekylmasser f.eks. kuldioxid, langsomt. Kalder man bølgelængden af en lydbølge dvs. afstanden fra bølgetop til bølgetop, for λ (måles i meter) og frekvensen for f Hz (måles i Hertz eller svingninger pr. sek.), gælder denne sammenhængen mellem v, λ og f:
\[ v = \lambda \cdot f \]
Høje toner har en høj frekvens. Det menneskelige øre kan høre frekvenser fra 20 Hz til 20 kHz, idet høreskader (for høj musik f.eks.) og alder efterhånden sænker den øvre grænse ganske væsentligt.

Uddybende Beskrivelse

Vi forstår normalt lyd som en bølgebevægelse, som breder sig i en gas. Det kan imidlertid også være bølgebevægelse i væsker og faste stoffer. I gasser og væsker breder lyden sig som en såkaldt longitudinalbølge, dvs. en bølge, hvor udbredelsesretningen er den samme som svingningsretningen  Bølgen indeholder energi, som følger bølgen.

I faste stoffer kan lyd også udbredes som en transversalbølge (Christophe Dang Ngoc Chan, Wikimedia Commons).

I faste stoffer kan det enten være longitudinalbølger, som i gasser, eller transversalbølger som havbølger, hvor bølgesvingningen er vinkelret på udbredelsesretningen.

I luft er lydhastigheden givet ved
\[v = \sqrt{\gamma\cdot\frac{p}{\rho}} = \sqrt{\frac{C_p}{C_v}\cdot\frac{p}{\rho}} \]
hvor \(\gamma = \frac{C_p}{C_v}\) (forholdet imellem en gas' varmefylde ved henholdsvis konstant tryk og rumfang), p er trykket og \(\rho\) gassens densitet, det giver 343m/s for atmosfærisk luft ved  20˚C og normalt tryk.

Lyd breder sig normalt kugleformigt ud fra lydkilden, og i fri luft aftager energien altså med kvadratet på afstanden. Ved forhindringer gælder de normale regler for bølger (bøjning og interferens), dvs. at de bølger, som er meget korte i forhold til forhindringens størrelse, bliver stoppet af hindringen, og der bliver derfor et 'lydskyggeområde' bag hindringen. Er hindringen lille i forhold til lydbølgelængden bøjes bølgerne om hindringen, og der bliver ikke et område, hvor lyden ikke høres.

Dette er grunden til, at man hjemme i stereoanlægget kan nøjes med én bashøjtaler ved musikgengivelse, fordi de dybe toner ikke indeholder meget retningsinformation, hvorimod høje toner skal komme fra hver sin højttaler. I små rum kan rummet begrænse den nedre grænse for musikgengivelsen, fordi tonernes bølgelængde kan være meget større end rummets største udstrækning, hvorfor tonen stort set fjernes ved interferens.

Man beskriver lydstyrke ved energitransporten, intensiteten, I, igennem en flade vinkelret på lydbølgen. Ved frekvensen f = 1000 Hz, kan et normalt menneskeligt øre lige opfange en intensitet I₀ = 10^-12 W/m².

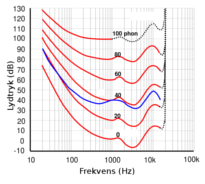
Oplevet lydniveau ved forskellig lydstyrke og frekvens (Linosland, Wikimedia Commons).

Man beskriver lydstyrke ved energitransporten, intensiteten, I, igennem en flade vinkelret på lydbølgen.

Ved frekvensen f = 1000Hz (1kHz) kan et normalt menneskeligt øre lige opfange en intensitet I₀ = 10^-12 W/m².  Vi kan høre frekvenser fra 20Hz til 20kHz, idet høreskader (fra for høj musik f.eks.) og alder efterhånden sænker den øvre grænse ganske væsentligt.

Vi angiver lydstyrken, som måles i Bell, ved størrelsen L, som defineres: \(L = \log\frac{I}{I_0}\), men normalt opgiver man den i stedet i decibel, dB, som er \(L = 10\cdot\log\frac{I}{I_0}\)dB.

Øret er ikke lige følsomt for alle frekvenser. Derfor skal der forskelligt lydtryk til for, at vi opfatter lyde med forskellige frekvenser som lige kraftige. Frekvensafhængigheden afhænger også af lydstyrken som vist i figuren

Malte Olsen