Temperatur

Grundbeskrivelse

Temperaturbegrebet bruges hyppigt i dagligdagen. Det optræder bl.a. i forbindelse med vejrudsigter og madlavning og man har en umiddelbar fornemmelse af, om der er varmt eller koldt i opgivelserne.

Temperatur er et mål for, hvor hurtigt molekyler bevæger sig. Her ses den termiske bevægelse af gasmolekyler.(Greg L, Wikimedia Commons).

Temperaturen i luften omkring os eller i en væske er et mål for den termiske energi i molekylerne, dvs. for, hvor hurtigt de bevæger sig. I faste stoffer bevæger molekylerne sig ikke frit rundt som i gasser og væsker, men vibrerer mere eller mindre kraftigt om deres position.

Som regel afhænger stoffers egenskaber meget af temperaturen. Det mest iøjnefaldende eksempel er faseovergange fra fast stof til væske og videre til gas, efterhånden som temperaturen stiger.Et mindre dramatisk eksempel er, at de fleste stoffer udvider sig, når temperaturen stiger.

I dagligdagen måler vi temperaturer i grader Celsius - forkortet ^oC. I fysiske, kemiske og andre videnskabelige sammenhænge bruges som regel absolut temperatur, som regnes fra det absolutte nulpunkt, der ligger ved -273,15^oC. Måleenheden for absolut temperatur er Kelvin, forkortet K. Man bruger ikke skrivemåden ^oK med gradtegn. Ved det absolutte nulpunkt 0K ligger molekylerne i følge den klassiske fysik stille men de har en ganske lille kvantefysisk nulpunktsenergi.

Uddybende beskrivelse

Strålingstemperaturen er en meget vigtig temperaturegenskab. Enhver overflade udstråler lys. Det er ikke nødvendigvis synligt lys, men kan også være langbølget infrarødt lys eller kortbølget ultraviolet lys. Det er mest forholdsvis varme overflader, der udsender lys, vi kan opfatte med vores sanser.

Varmer man et stykke metal en smule op, kan man mærke at det udstråler varme - infrarød stråling - når man holder hånden hen i nærheden af overfladen. Når man varmer det mere op, bliver det rødglødende. Det begynder at udsende synligt lys i den langbølgede røde del af spektret. Ved opvarmning til en endnu højere temperatur - når metallet bliver hvidglødende - bliver lyset kraftigere og mere hvidligt. Det hvide lys indeholder mere kortbølget lys end det røde.

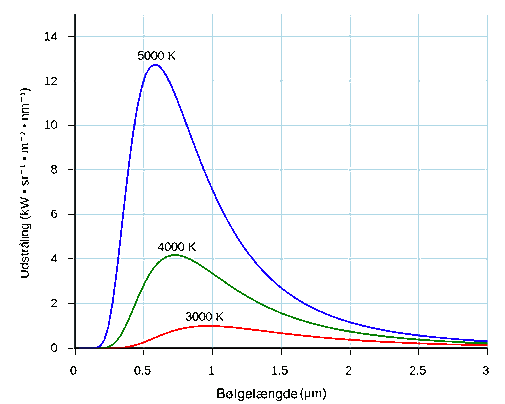
Planck-kurver for tre temperaturer (Darth Kule, Wikimedia Commons).

Både lysstyrken og bølgelængdefordelingen afhænger altså af temperaturen. Det beskrives ofte ved en familie af kurver med en kurve for hver temperatur. En højere temperatur giver en kurve, der dels ligger højere og dels med toppen ved en kortere bølgelængde en kurven for en lavere temperatur. Kurverne kaldes Planck-kurver efter den tyske fysiker Max Planck.

Bølgelængden \(\lambda_{max}\) for toppen af kurven er omvendt proportional med den absolutte temperatur T: \[\lambda_{max} = b\cdot\frac{1}{T}\] hvor proportionalitetskonstanten b = \(2,9\cdot 10^{-3}\)m·K kaldes Wiens konstant efter Wilhelm Wien, der beregnede den i 1893.

Denne sammenhæng udnyttes i energiruder - glas, der er belagt med et filter, der blokerer for langbølget infrarød stråling. Solens overfladetemperatur er omkring 6000K, så den lyser mest ved bølgelængder omkring 500nm - lys, der uhindret går gennem ruden. Stuetemperatur på Jorden er knap 300K, en tyvendedel af Solens temperatur. Derfor udsender vores stuer infrarød stråling med bølgelængder på omkring tyve gange sollysets: 10μm. Det stoppes af rudens filter, som på den måde holder på varmen.

Lysstyrken - den udsendte strålingseffekt pr kvadratmeter - I er proportional med den absolutte temperatur T i fjerde potens: \[I = \sigma \cdot T^4\] Denne sammenhæng kaldes Stefan-Boltzmanns lov og proportionalitetskonstanten \(\sigma = 5,67 \frac{W}{m^2K^4}\) kaldes Stefan-Boltzmanns konstant efter de fysikere, der har beskæftiget sig med emnet i slutningen af 1800-tallet.

Regneudtrykket for Planck-kurverne er noget mere kompliceret. Sammenhængen mellem temperaturen T, bølgelængden \(\lambda\) og energiudsendelsen \(u(\lambda,T)\) ved forskellige bølgelængder ser sådan ud: \[ u(\lambda,T) = \frac{2hc^2}{\lambda^5}\cdot\frac{1}{e^{\left({\frac{hc}{kT\lambda}}\right)} -1} \], hvor \(h = 6,62 \cdot 10^{-34}\)J·s er Plancks konstant, \(c = 3 \cdot 10^8\)m/s er lyshastigheden og \(k = 1,38 \cdot 10^{-23}\)J/K er Boltzmanns konstant.

Denne sammenhæng blev opdaget af i 1900 af Max Planck og var et pionerarbejde i starten af kvantefysikken.

Michael Quaade