Cirkelbevægelser

Grundbeskrivelse

Når noget med masse bevæger sig i en bane med en konstant afstand til et fast midtpunktet, kaldes det en cirkelbevægelse.

For eksempel kredser satelliter om Jorden i en jævn cirkelbevægelse, og Jorden udfører med god tilnærmelse en jævn cirkelbevægelse om Solen.

I en cirkelbevægelse går kraften, kaldet centripetalkraften, indad! Det kan være lidt sært ved første øjekast, men ser man på for eksempel Jordens omløb om Solen, vil Solen trække i Jorden med samme kraft som jorden trækker i solen. Den resulterende kraft på jorden vil derfor pege mod Solens centrum hele tiden.

Man kan sige, at grunden til, et objekt kan fastholdes i en cirkelbevægelse er, at det konstant kraft imod centrum, men med en fart vinkelret på radius. Eksempel når man svinger et lod rundt i en snor trækker hånden i snoren og giver via snoren den nødvendige centripetalkraft til at få loddet til at bevæge sig i en cirkel. Skæres snoren over, fortsætter loddet efter en ret linje i den retning det havde, da snoren sprang.

Uddybende beskrivelse

Jævn cirkelbevægelse:

For at kunne udføre en jævn cirkelbevægelse må objektet have en konstant hastighed v, der altid er tangent til cirkelbanen, det bevæger sig på.

Man kan forestille sig et fly, der kredser om det samme punkt med konstant vinkelhastighed \(\omega\), afstand r og højde over jordens overflade.

Tyngdekraften udlignes af den opløftende kraft på flyets vinger, så den kan man se bort fra. Kraften og hastigheden vil være konstant, men hele tiden ændre retning.

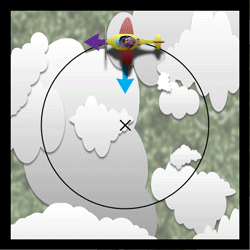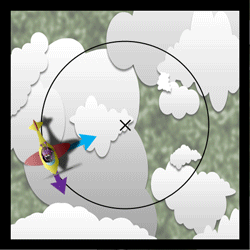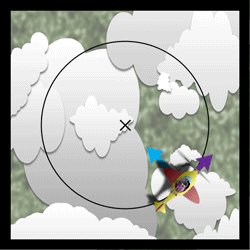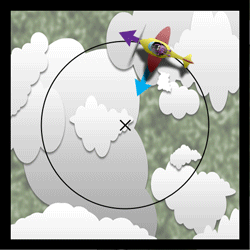
Fly i jævn cirkelbevægelse. Centrum af banen er markeret med X, blå pil angiver centripetalkraften \(F_{cen}\). Lilla pil hastigheden v. (Chano Birkelind)

Centripetalkraften er da

\[F_{cen}=m \frac{v^{2}}{r}=m \omega^{2}r\]

Ujævn cirkelbevægelse:

Man kan også have det, der kaldes ujævn cirkelbevægelse. Her kredser objektet stadig i en fast bane, men vinkelhastigheden er ikke længere konstant.

Man kan forestille sig en bille, der er fastgjort på et oprejst hjul, som drejer. 

Ujævn cirkelbevægelse. Billens hastighed varierer, men den holdes stadig i en cirkulær bane. (Chano Birkelind)

Hvis man deler accelerationen op i den indadgående centripetal-acceleration og den tangentielle, vil man se, at den effektive acceleration ikke peger mod centrum længere, men varierer med billens position. 

På vej ned vil den tangentielle acceleration øges billens hastighed. Hvorimod den vil blive bremset ned, når den er på vej op, fordi den tangentielle acceleration nu peger modsat billens bevægelsesretning. Det betyder, at centripetalaccelerationen er størst i bunden og mindst i toppen. Mens den tangentielle acceleration er nul begge steder.   

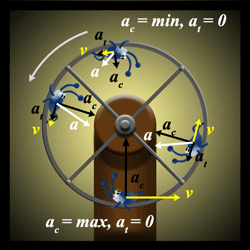
Øjebliksbillede af billen i forskellige positioner på hjulet. Den effektive acceleration a kan opdeles i Centripetalaccelerationen \(a_{c}\) og tangtielaccelerationen \(a_{t}\). (Chano Birkelind)

Det er nemmest at se, hvis man tænker på accelerationen som vektorer. En vektor er en størrelse med en retning, og man kan så dele accelerationen op i hhv. centripetal og tangtentiel acceleration. Disse vil være vinkelret på hinanden, men den resulterende effektive acceleration vil ændre retning, som billen roterer og kun pege mod centrum, når billen befinder sig øverst og nederst i banen.

Fordi den tangentielle acceleration er forskellig fra nul, er billen altså påvirket af flere kræfter end centripetalkraften.
I dette tilfælde er både tyngdekraften, normalkraften og gnidningskraften en vigtig faktor.

Summen af alle kræfter, der påvirker billen, må være lig centripetalkraften.

\[F_{total}=F_{cen}\]

Da billen ellers ikke vil fortsætte i cirkelbevægelsen. 

Chano Birkelind