Magnetfelter og højrehåndsregler

Grundbeskrivelse

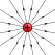
Magnetfeltetrs retning omkring en strømførende ledning. (Chano Birkelind).

En elektrisk ladning, der bevæger sig, vil frembringe et magnetisk felt, der er rettet rundt om bevægelsesretningen. Det er på den måde, der opstår et magnetfelt rundt om en strømførende ledning.

Retningen af magnetfeltet B omkring en ledning, hvor der løber en strøm I kan man finde ved hjælp af en højrehåndsregel:

• Hold om ledningen - eller ladningens bevægelsesretning - med højre hånd og
  tommelfingeren i strømmens - eller ladningens retning. Magnetfeltet er da rettet i fingrenes retning.

Her forudsættes, at der er tale om en positiv ladning, der bevæger sig. En negativ ladning - f.eks. en elektron - vil give et magnetfelt den modsatte vej rundt om bevægelsesretningen. Dette stemmer overens med, at strøm i én retning i en ledning i virkeligheden er bevægelse af elektroner den modsatte vej i ledningen.

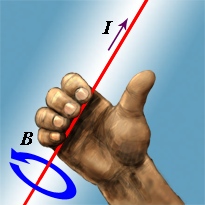
En elektrisk ladning, der bevæger sig i et magnetfelt, vil blive påvirket af en kraft, der er på tværs af både magnetfeltet og bevægelsesretningen. Retningen kan ligeledes findes med en højrehåndsregel:

• Hold højre hånd, så tommel-, pege- og langfinger er nogenlunde vinkelrette på hinanden.
  En positiv ladning, der bevæger sig i tommelfingerens retning i et mangetfelt rettet langs pegefingeren, vil blive påvirket af en kraft i langfingerens retning.

Der findes adskillige andre højrehåndsregler, men de kan alle opfattes som
varianter af disse to.

Uddybende beskrivelse

Matematisk er den sidste af de to ovenstående højrehåndsregler et eksempel på krydsprodukt af to vektorer. En vektor er karakteriseret ved både at have en størrelse og en retning. Der findes massevis af fysiske begreber, som er vektorer, f.eks. hastigheder, felter og kræfter der alle tre indgår i beskrivelsen af en elektrisk ladning, som bevæger sig i et magnetfelt. Derimod er elektrisk ladning ikke en vektor, men en skalar. Den har ikke nogen retning, men er alene beskrevet ved sin størrelse og fortegn - der findes både positive og negative ladninger. Andre eksempler på skalarer fra fysikkens verden er masse og energi.

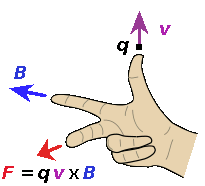
Højrehåndsreglen viser retningen af den kraft, der påvirker en elektrisk ladning, der bevæger sig i et magnetfelt. (Acdx, Wikimedia Commons).

Det matematiske udtryk for den kraft \(\vec{F}\), der påvirker en ladning \(q\), der bevæger sig med hastigheden \(\vec{v}\) i et magnetfelt \(\vec{B}\), ser sådan ud:
\[ \vec{F} = q \vec{v} \times \vec{B} \]
Krydset og betegnelsen krydsprodukt angiver, at resultatet - i dette tilfælde \(\vec{F}\) - er en vektor, der er vinkelret på både \(\vec{v}\) og \(\vec{B}\). Retningen er som beskrevet ved højrehåndsreglen. Bemærk, at rækkefølgen af de to vektorer, der indgår i krydsproduktet, er vigtig. Den første skal pege i tommelfingerens retning og den anden i pegefingerens retning. Hvis de byttes om, bliver resultatet en vektor, der peger den modsatte vej.

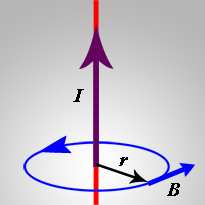
Beregning af magnetfeltet omkring en strømførende ledning. (Chano Birkelind).

Ved første øjekast ser den første af de to højrehåndsregler enklere ud. Til gengæld bliver situationen noget mere kompliceret, når man begynder at regne på tingene. Det er kun simpelt og overskueligt i det meget forenklede eksempel, at vi ser på magnetfeltet langs en cirkel omkring en i princippet uendelig lang og lige ledning. Her gælder den simple sammenhæng:  
er magnetfeltet et givet sted på cirklen, \(\vec{I}\) er strømmen, \(\vec{r}\) er radius i cirklen som en vektor rettet fra cirklens centrum på ledningen til det punkt, vi betragter, og \(\mu_0\) er den magnetiske feltkonstant eller vakuumpermeabiliteten, en konstant hvis værdi er definitionsmæssigt fastsat til \(4\cdot\pi\cdot10^{-7}\frac{\text{N}}{\text{A}^2}\).

Michael Quaade