Keplers love
 Grundbeskrivelse
Grundbeskrivelse
I starten af 1600-tallet fandt Johannes Kepler frem til sine tre love på grundlag af Tycho Brahes meget præcise observationer af planeten Mars' position på himlen. Lovene drejer sig om planetbaners form og planeternes hastigheder i banerne.
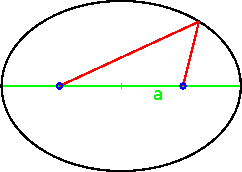
En ellipse. Summen af afstandene - de røde linier - fra et punkt på ellipsen til de to brændpunkter - de blå cirkler - er den samme. Den grønne linie kaldes ellipsens storakse. Halvdelen af storaksen kaldes a og kan sammenlignes med radius i en cirkel. (Michael Quaade).
I følge Keplers første lov er planetbanerne ellipseformede og Solen er i ellipsens ene brændpunkt. Summen af afstandene fra en ellipses to brændpunkter til et punkt på ellipsen er den samme hele vejen rundt. Den er også den samme som ellipsens største diameter - den kaldes ellipsens storakse. En cirkel kan opfattes som et specialtilfælde af en ellipse, hvor de to brændpunkter falder sammen i cirklens centrum.
En planet bevæger sig hurtigere når den er tættere på Solen. Det viser sig dels ved at hver enkelt planet bevæger sig hurtigst i den del af ellipsebanen, der er nærmest ved Solen og dels ved at en planet med en bane tæt på Solen bevæger sig hurtigere end en planet med en større bane langt fra Solen.
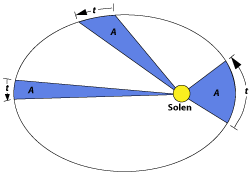
Keplers anden lov. I løbet af en given tid t bevæger planeten sig længst i sin bane, når den er tættest på Solen. (Wikimedia Commons)
Keplers anden lov beskriver hastighedsændringerne for en planet i forskellige steder i dens bane. Vi ser på, hvor stort et "lagkagestykke" planeten skærer ud af ellipsebanen i løbet af et givet stykke tid t - f.eks. en uge eller en måned. Det er de blå arealer A på tegningen til højre. Keplers anden lov siger, at arealerne A er lige store for samme tid t uanset hvor i banen planeten befinder sig.
Keplers tredje lov handler om sammenhængen mellem omløbstid og banens størrelse for forskellige planeter i Solsystemet. \[ T^2 = a^3 \] hvor omløbstiden T måles i år og banens halve storakse a - se den øverste tegning - måles i astronomiske enheder - jordbanens halve storakse.
 Uddybende beskrivelse
Uddybende beskrivelse
Kepler fandt frem til sine love udelukkende ud fra Tycho Brahes observationer af planeternes positioner på himlen. Det har siden vist sig, at de var naturlige følger af mere grundlæggende fysiske love.
Det var primært Isaac Newton, der påviste disse sammenhænge. Han udgav i 1687 - mange år efter Keplers død - sit berømte værk Philosophiæ Naturalis Principia Mathematica på latin. Titlen betyder naturfilosofiens matematiske principper og det indeholdt bl.a. Newtons tyngdelov: \[ F = G\cdot \frac{M_1\cdot M_2}{r^2} \] hvor F er tyngdekraften mellem to masser \(M_1\) og \(M_2\) med afstanden r. G er gravitationskonstanten, 6,67\(\cdot 10^{-11}\frac{\mathrm{N\cdot m^2}}{\mathrm{kg^2}}\). Det centrale indhold i Newtons tyngdelov er, at tyngdekraften mellem to legemer aftager med kvadratet på deres afstand. For en planet i Solsystemet er de to masser Solens masse \( M_\odot \) og planetens egen masse \( M_p \).
Når to kloder svæver frit i rummet og ikke påvirkes af andet end deres gensidige tyngdekraft, vil det resultere i, at de kan kredse om hinanden i stabile elliptiske baner, der beskrives ved Keplers love.
Strengt taget kredser de om deres fælles tyngdepunkt, men i Solsystemets tilfælde vejer Solen så meget mere end alle planeterne, at man med god tilnærmelse kan regne med, at planeterne kredser om Solen, der ligger stille. Det er heller ikke kun massetiltrækningen fra Solen, der styrer planetens baner - de påvirker også hver især gensidigt hinanden med deres egen tyngdekraft. Men også her gælder det, at Solens masse er så meget større end alle planeternes masser tilsammen at det hovedsagelig er dens tyngdekraft, der spiller en rolle.
Keplers anden lov er en følge af, at impulsmomentet er en bevaret størrelse, der ligesom f.eks. energi ikke kan opstå eller forsvinde. Det er en tilsvarende mekanisme der er i spil, når en skøjteløber eller balletdanser laver pirouetter. Når man laver en pirouette, starter man med at rotere langsomt med udtstrakte arme. Derefter trækker man armene ind mod kroppen, hvorved rotationshastigheden øges.
Impulsmomentet L for en planet i dens bane beregnes på denne måde: \[L = M_p\cdot r\cdot v\] hvor \( M_p \) er planetens masse, r dens aktuelle afstand fra Solen og v dens banehastighed - mere præcist den komponent af hastigheden, der er vinkelret på retningen til Solen. Når planeten nærmer sig Solen bliver r mindre, og v vokser da tilsvarende, så L holdes konstant.
Keplers tredje lov er også en direkte følge af Newtons tyngdelov. Det er nemmest at se for en cirkulær bane, men det gælder også for ellipsebaner.
En planet, der bevæger sig i en cirkelbevægelse om Solen, holdes i sin bane af en centripetalkraft rettet mod centrum. Centripetalkraften \( F_c \) kan beregnes på denne måde: \[ F_c = M_p\cdot\frac{4\pi^2}{T^2}\cdot r \] hvor \( M_p \) er planetens masse, P dens omløbstid og r dens baneradius. Centripetalkraften er tyngdekraften fra Solen som beskrevet ovenfor med masserne af Solen, \( M_\odot \), og planeten, \( M_p \), indsat: \[ F = G\cdot \frac{M_\odot\cdot M_p}{r^2} \] Når de to kræfter er den samme, \( F = F_c \), kan de to regneudtryk kombineres til: \[ G\cdot \frac{M_\odot\cdot M_p}{r^2} = M_p\cdot\frac{4\pi^2}{T^2}\cdot r \] der kan omskrives til: \[ \frac{T^2}{r^3} = \frac{4\pi^2}{G \cdot M_\odot} \] Alt på højre side af lighedstegnet er konstant - når vi ser på planeter i samme solsystem, så det er samme \( M_\odot \). Det betyder, at forholdet mellem \( T^2 \) og \( r^3 \) er konstant.
I en ellipse erstattes banens radius r med a, den halve storakse. Det giver lidt mere omstændelige beregninger, men resultatet er det samme.
Det er nemt at slippe for at finde proportionalitetskonstanten, hvis man måler omløbstiden P i år og banens halve storakse a i astronomiske enheder - jordbanens halve storakse. Det er jo velkendt, at Jordens omløbstid er ét år og den er pr. defintion én astronomisk enhed fra Solen, så proportionalitetsfaktoren bliver 1 for Jorden - og derfor også for de andre planeter i Solsystemet. Det fører frem til at Keplers tredje lov kan skrives på den nemme form: \[ P^2 = a^3 \] I vore dage kender man massevis af planeter, der kredser om andre stjerner end Solen. Her kan man udvide Keplers tredje lov, så massen af stjernen \( M_\star \) tages med: \[ P^2 = \frac{a^3}{M_\star} \] Ligesom P og a måles i år og astronomiske enheder, skal \( M_\star \) måles i solmasser, \(M_\odot \). Solens masse på knap \(2\cdot 10^{30}\)kg er en almindeligt anvendt masseenhed indenfor astronomi.
Keplers love gælder ikke bare for planeterne i Solsystemet, men også for f.eks. de måner, der kredser om en planet og satellitter, der er i kredsløb omkring Jorden - men her skal man på samme måde tage højde for massen af den centrale klode når man beregner sammenhængen mellem P og a.
Michael Quaade
Vælg en kategori