Impuls (bevægelsesmængde)

Grundbeskrivelse

Et legemes impuls p er bestemt som legemets masse m gange legemets hastighed v:

\[ p = m \cdot v \]

Retningen på impulsen er den samme som retningen på hastigheden.

Et tog, der vejer 100 tons og kører 100 km/t, har den dobbelte impuls af et tog, der vejer 100 tons og kører 50 km/t, mens et tog, der vejer 200 tons og kører 100 km/t, har den firedobbelte impuls af et tog, der vejer 100 tons og kører 50 km/t.

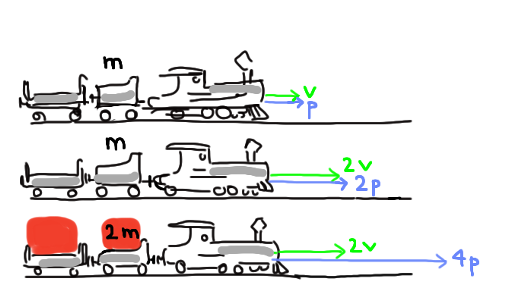
Impulsen p afhænger af hastigheden v og massen m. (Peter Ditlevsen)

Et legemes impuls ændrer sig ikke, hvis ikke legemet påvirkes af ydre kræfter (Newtons første lov). Vi siger, at impulsen er en bevaret størrelse. Hvis et legeme påvirkes af kræfter, ændres impulsen (Newtons anden lov), tilsvarende ændrer impulsen sig nøjagtigt lige så meget og i modsat retning for det andet legeme, som udfører kraften, således at den samlede impuls ikke ændrer sig. Dette er "loven om aktion og reaktion" (Newtons tredje lov). Impuls kan kun flyttes fra et legeme til et andet, impulsen kan aldrig forsvinde eller opstå.

Peter Ditlevsen

Uddybende beskrivelse

Når ingen ydre kræfter påvirker et system, er impulsen en bevaret størrelse. To legemer kan godt overføre impuls mellem sig igennem et stød, men den samlede impuls er den samme før og efter stødet. Forestil dig et billardbord med kugler, der alle ligger stille. De har ingen hastighed og dermed ingen impuls. Hvis du nu støder til den hvide kugle, påvirkes den kortvarigt udefra med en kraft, der giver den en impuls og den triller hen ad bordet. Den hvide kugle rammer den sorte kugle i et centralt elastisk stød og overfører derved impuls til den sorte kugle. Den hvide kugle ligger nu stille, mens den sorte kugle triller videre med netop den impuls (altså fart og retning), du gav den hvide kugle.

Bevarelse af impuls i et system, hvor man kan se bort fra ydre kraftpåvirkninger, kan bruges til at beregne f.eks. to legemers hastigheder efter deres sammenstød. For et sammenstød mellem to legemer med masserne \(m_{1}\) og \(m_{2}\) siger princippet om impulsbevarelse, at den samlede impuls af de to legemer skal være den samme før og efter stødet. Impuls kan altså overføres mellem legemerne, men ikke opstå eller forsvinde. Impulsbevarelsen for et sammenstød mellem to legemer med masserne \(m_1\) og \(m_2\) kan udtrykkes i følgende formel:
\[ m_1 \cdot \vec{v_1} + m_2 \cdot \vec{v_2} = m_1 \cdot \vec{u_1} + m_2 \cdot \vec{u_2} \]
hvor v er hastigheder før sammenstødet og u er hastigheder efter. Pilene angiver at hastighederne er vektorer - de har både en størrelse og en retning.

Atlas V-raket på vej til Mars med Curiosity-roveren ombord. Forbrændingsprodukternes bagudrettede impuls giver raketten en fremadrettet impuls. (NASA/George Roberts)

Impulsbevarelse bruges i et utal af sammenhænge inden for fysik, og er bl.a. nøglen til at forstå, hvordan en raket accelererer.

Forestil dig, at en raket affyres ude i rummet, langt fra planeter, der kunne påvirke den med massetiltrækning. Når der ingen ydre kræfter er, er impulsen af systemet bevaret. I udgangspunktet holder raketten stille, dvs. den samlede impuls af systemet er 0.

For at kunne bevæge sig fremad må raketten brænde en masse brændstof af. Det brugte brændstof sendes derved bagud fra raketten med stor hastighed. Det brugte brændstof har altså nu en impuls i retning bagud fra raketten. Men da impulsen er bevaret, skal den samlede impuls af system fortsat være 0 ligesom i udgangspunktet.

Derfor får raketten nu en lige så stor impuls som brændstoffet, blot i den modsatte retning, nemlig fremad. Dermed er summen af de to impulser 0, og den samlede impuls er bevaret.

Situationen er i realiteten lidt mere kompliceret, fordi rakettens masse ændres, efterhånden som den opbruger brændstoffet, men det grundlæggende princip er stadig impulsbevarelse.

Impulsen af et legeme eller en partikel er generelt en vektor, der har samme retning som hastighedsvektoren:
\[ \vec{p} = m \cdot \vec{v}\]
Impulsen af et legeme ændres, hvis legemet påvirkes af kræfter. Hvis legemet starter med at ligge stille og påvirkes af en konstant kraft \(\vec{F}\) i et stykke tid t vil det opnå en impuls \(\vec{p}\), der kan beregnes på denne måde:
\[ \vec{p} =\vec{F}\cdot t \]
Ændringen af et legemes impuls hænger således sammen med kraften, der påvirker det, og den tid, påvirkningen varer.

Cecilia Mortensen Kobæk