Fiktive kræfter
 Grundbeskrivelse
Grundbeskrivelse
Hvordan kan det være, at hvis vi sidder i en bil, der bremser, så mærker vi en kraft, der trækker os fremad? Eller hvorfor er vi ved at blive slynget af en roterende karrusel? Svaret skal findes i de såkaldte fiktive kræfter eller inertikræfter, som de også kaldes.
Med begrebet fiktive kræfter skal forstås, at der ikke er en fysisk årsag, som tyngdekraften, men derimod en effekt, der ses, når man befinder sig i et accelereret system som for eksempel i en elevator eller en bil, der accelererer. Der er derfor tale om kræfter, der kun mærkes, når man befinder sig i et system, der er i bevægelse, og ikke opdigtede kræfter.
 Uddybende beskrivelse
Uddybende beskrivelse
Elevatorkraften
For at forstå hvad elevatorkraften er, kan vi kigge på en stillestående elevator med en bille i. Elevatoren begynder nu at køre op.

Elevatorkraften. Elevatoren sætter i gang opad og har dermed en opadrettet acceleration. Billen mærker gulvet trykke mod den nedefra og det føles som om tyngdekraften er blevet større.(Chano Birkelind)
Elevatorkabinen bevæger sig op med en acceleration fra omgivelserne. Men billen opfatter det som om, at elevatoren står stille og mærker kraften \(F = m\cdot a\) som en større tyngdekraft rettet mod elevatorens bund, fordi det er den kraft, som gulvet presser med på dens fødder.
Et andet eksempel er en bil, der accelererer fremad. Man vil føle, at man presses bagud i sædet, men egentlig er det fordi sædet trykker mod ens ryg.
Centrifugalkraften
Hvis man, med en konstant vinkelhastighed \(\omega\) svinger en spand i en afstand r, hvori der sidder en bille med massen, m, vil den ikke falde ud, men derimod blive presset mod bunden af spanden, som om en kraft prøver at slynge den væk fra centrum af rotationen.

Centrifugalkraften. En spand er bundet fast i en snor og svinges rundt. I spanden er en bille. Udefra kan man se billen + spand som en samlet masse, og den eneste kraft, der påvirker dem, er den indadrettede centripetalkraft (rebets trækkraft). Inde i spanden mærker billen kun centrifugalkraften presse den mod bunden af spanden (orange pil), men spanden og billen selv står stille. (Chano Birkelind).
Set inde fra spanden ligger billen stille. Måler vi til gengæld kraften på billen, kan vi se, at den trykkes udad med en kraft \[F_{cen} = m{\omega}^{2}r\] hvilket er centrifugalkraften. Tilsvarende trykker spandens bund tilbage med en lige så stor modsat rettet kraft. Derfor mærker billen en form for tyngdekraft inde i spanden. Det er det samme, der sker, når vaskemaskinen centrifugerer tøjet, og derfor man kan hænge med hovedet nedad i et loop i en rutchebane i en forlystelsespark. I teorien ville man også kunne lave rumstationer med kunstig tyngdekraft ud fra dette princip.
Corioliskraften
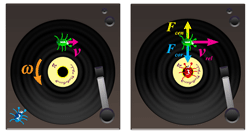
Corioliskraften. De to situationer, der er vist, er hhv.: Venstre: set fra den blå bille (bille 2) på pladespilleren og højre: Set fra den røde bille (bille 3), der roterer med pladen. For den blå bille roterer pladen med vinkelhastighed \(\omega\) og den grønne bille (bille 1), der bevæger sig med en passende hastighed \(v\) modsat omdrejningsretningen, står stille. For den røde bille står pladen stille, og den grønne bille bevæger sig i et kredsløb med hastigheden \(v_{rel}\) og er påvirket af kræfterne \(F_{cen}\) og \(F_{cor}\) (Chano Birkelind).
En måde at forklare Corioliskraften er ved at forestille sig biller på en gramofonplade.
Pladen roterer mod uret, mens bille 1 bevæger sig med uret med samme hastighed. For tilskueren, bille 2, står bille 1 stille, hvis vi forestiller os, at gnidningskraften på bille 1 er så lille, at vi kan se bort fra den.
Men hvis vi nu ser bevægelsen fra bille 3, der drejer rundt med pladen uden at bevæge sig, vil bille 1 se ud til at være i kredsløb om pladens midtpunkt med en relativ hastighed, der er en sum af dens egen hastighed og pladens omdrejningshastighed i billens afstand fra centrum, men med modsat fortegn \(v_{rel} = v + (-v_{r})\)
Der må altså være nogle kræfter, der holder bille 1 i kredsløb om pladens centrum. Da der ikke er nogen tyngdekraft, snore eller andet, må det skyldes de fiktive kræfter. Centrifugalkraften, der trækker billen udad og corioliskraften, der i dette tilfælde trækker billen indad.
Corioliskraften peger til højre, hvis man bevæger sig ovenpå en disk, der roterer mod uret og den er altid vinkelret på hastigheden og omdrejningsaksen. Den defineres matematisk (numerisk) som: \[F_{cor} = -2m(\omega \cdot v_{rel})\] Hvor \(F_{cor}\) er corioliskraften, m massen af billen, \(\omega\) er pladens vinkelhastighed og \(v_{rel}\) er billens relative hastighed i forhold til det roterende system. Det vil sige, at corioliskraften er afhængig af hastighedens størrelse og retningen.
Hvis billen i ovenstående eksempel havde prøvet at bevæge sig udad, ville den opleve, at pladen flytter sig hurtigere og hurtigere mod uret, jo længere væk fra centrum den kommer. Corioliskraften vil derfor blive større og større, og billen i midten af pladen ville opleve at bille 1 bliver accelereret med urets retning.
Det er nøjagtigt det samme, der skernår lav eller højtryk eller når skyer, bevæger sig fra nord mod syd henover jordens overflade.
Chano Birkelind
Vælg en kategori